機器學習基本概念簡介
什麼是機器學習?
機器學習可以用一句話概括:讓機器具備「找一個函式 (Function)」的能力。
常見的任務類型
-
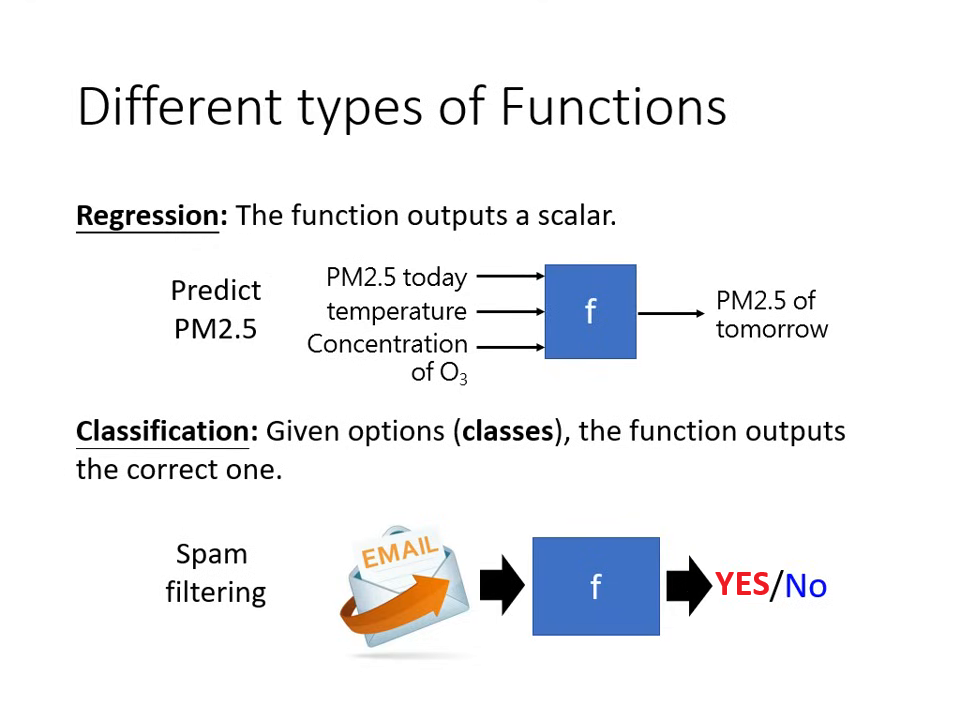
迴歸 (Regression):函式的輸出是一個
數值 (Scalar)(例如:預測明天的 PM2.5 數值)。 -
分類 (Classification):讓機器做「選擇題」。我們會先
準備好選項(類別),機器從中選出正確答案(例如:垃圾郵件偵測、AlphaGo 下棋的落子位置)。 -
結構化學習 (Structured Learning):機器不只是做選擇,而是要產生有結構的物件(例如:畫一張圖、寫一篇文章),這可以被稱為讓機器學會「創造」。
機器學習的三個步驟
假設我們想找出一個函式,其輸入是 YouTube 後台資訊,輸出是隔天的總點閱率。
第一步:寫出帶有未知參數的函式 (Model)
我們需要根據 Domain Knowledge 先猜測函式的樣子。
- 模型 (Model):例如 ,這是一個帶有未知參數的函式。
- 特徵 (Feature):已知的資訊(例如前一天的點閱人數 )。
- 權重 (Weight, ) 與 偏置 (Bias, ):這是機器需要透過資料找出的未知參數 (Parameter)。

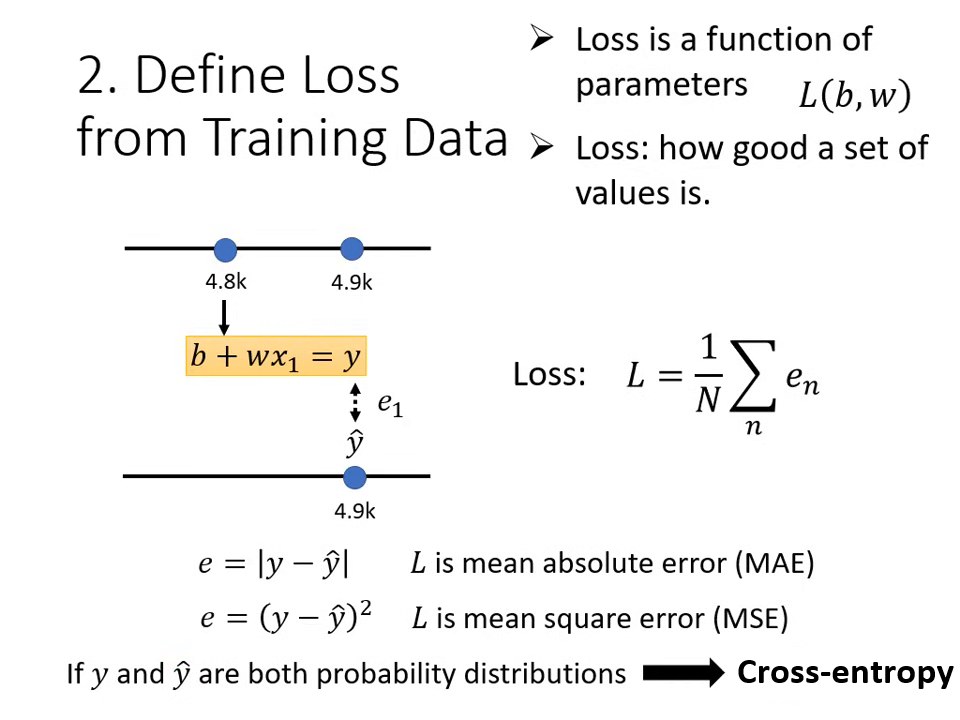
第二步:定義損失函數 (Loss Function)
損失函數 是一個用來評估參數好壞的函式,其輸入是參數,輸出代表這組參數有多「不準」。
- 計算方式:比對預測值 () 與真實值 (標籤 Label, ) 的差距。
- MAE (Mean Absolute Error):計算差距的絕對值。
- MSE (Mean Square Error):計算差距的平方。
- 誤差表面 (Error Surface):將不同的 與 組合對應的 Loss 畫成等高線圖。顏色越偏藍代表 Loss 越小(參數越好)。
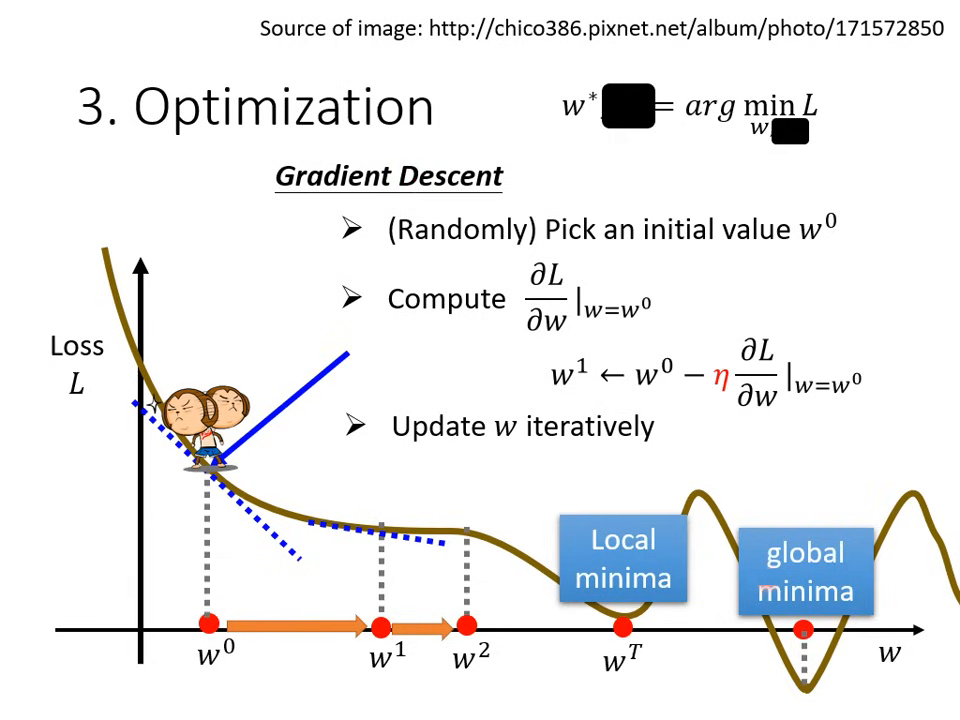
第三步:解最佳化問題 (Optimization)
目標是找到一組 與 ,讓 Loss 的值最小。
-
梯度下降 (Gradient Descent):
- 隨機初始化:隨機選一個起始點 。
- 計算微分 (Gradient):計算該點的切線斜率。斜率為負則增加 ,斜率為正則減少 。
- 更新參數:更新的大小取決於斜率與 學習率 (Learning Rate, )。
-
超參數 (Hyperparameter):由人類手動設定而非機器找出的數值(如:學習率、更新次數)。
線性模型 (Linear Model)
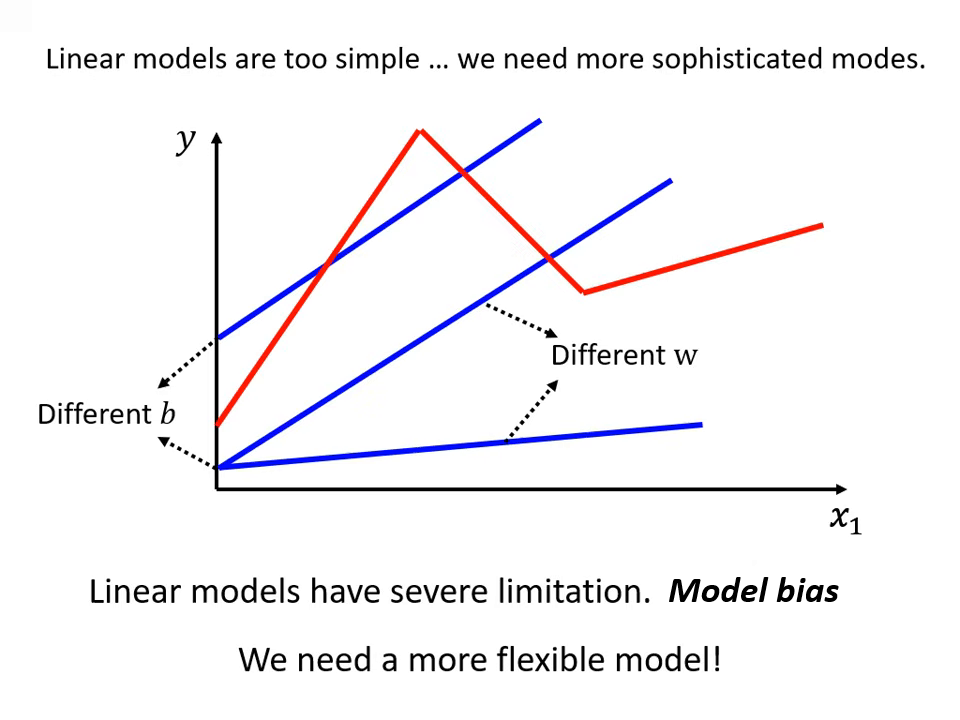
線性模型的限制與模型偏差 (Model Bias)
線性模型(Linear Model)假設特徵 與輸出 之間僅存在直線關係。
- 問題點:現實中的關係可能非常複雜,例如觀看人數過高後可能物極必反地下降,直線模型無論如何調整參數 與 ,都無法畫出帶有轉折的曲線。
- 模型偏差 (Model Bias):這種來自於模型過於簡單、無法模擬真實狀況的限制,稱為 Model Bias。
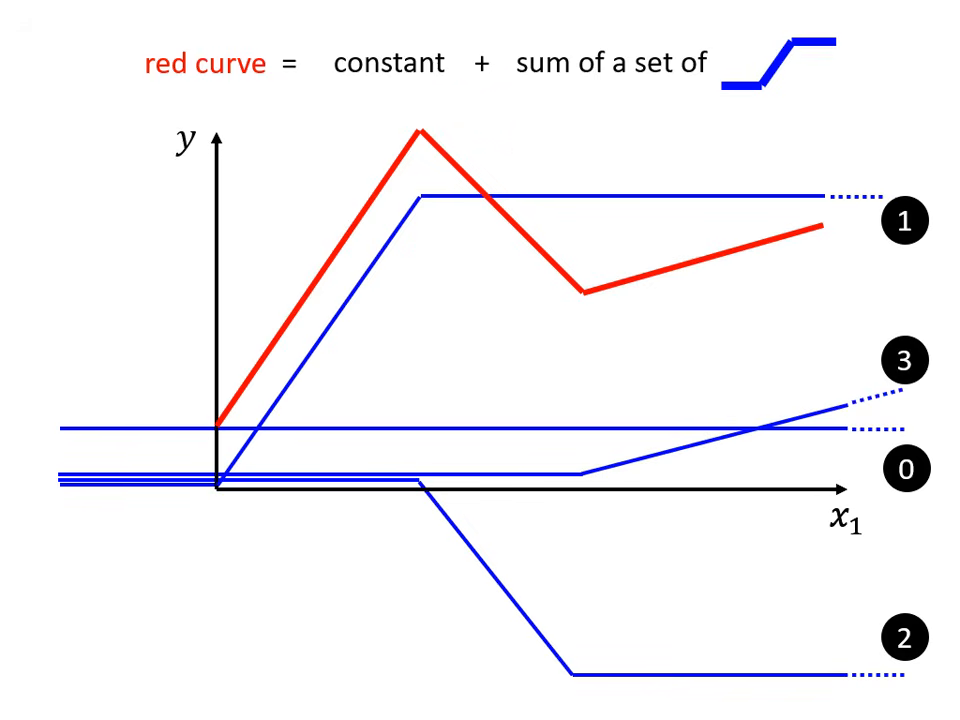
分段線性曲線 (Piecewise Linear Curves)
為了減少 Model Bias,我們需要更有彈性的函式。
- 原理:複雜的紅色彩色曲線可以看作是一個常數加上一群藍色的「硬激活函數」 (Hard Sigmoid)。
- 藍色函數特性:先水平、再斜坡、最後再水平。透過調整斜坡的起點、終點與斜率,可以拼湊出任何鋸齒狀的折線圖。
- 逼近任何曲線:只要轉折點夠多(使用的藍色函數夠多),分段線性曲線就可以逼近任何連續的曲線。
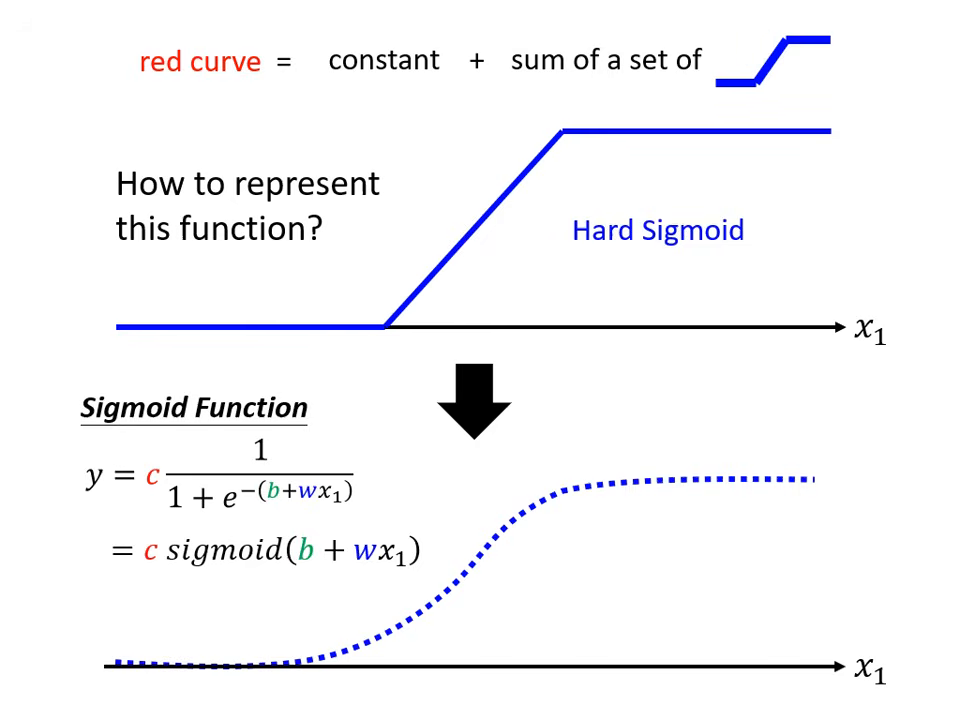
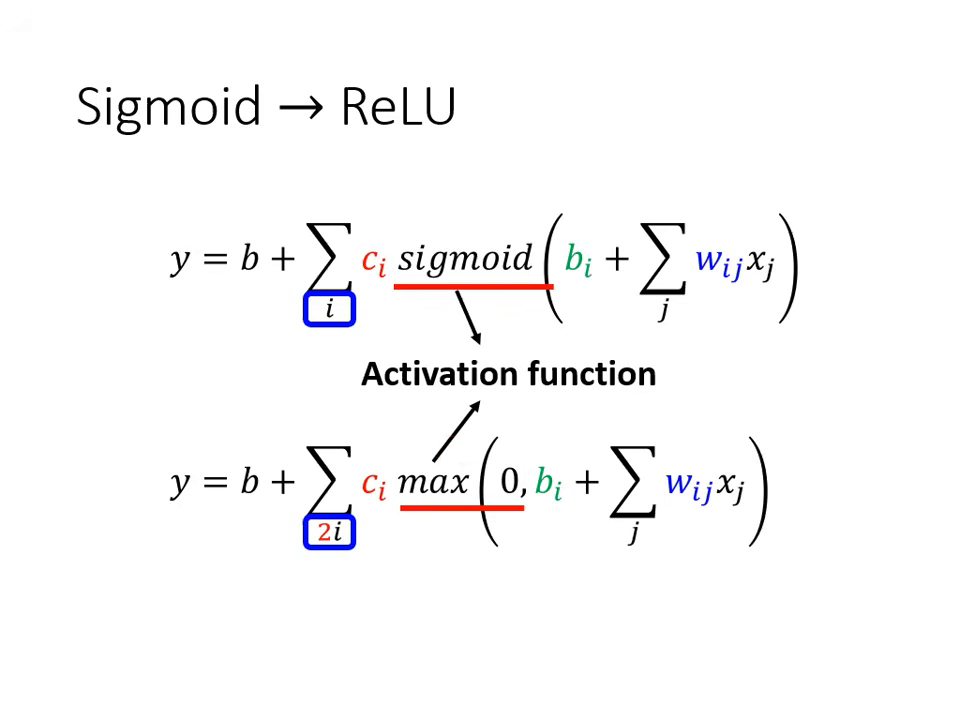
激活函數 (Activation Function):Sigmoid 與 ReLU
由於 Hard Sigmoid 難以直接寫出數學式,實務上會使用平滑的函數來逼近它。
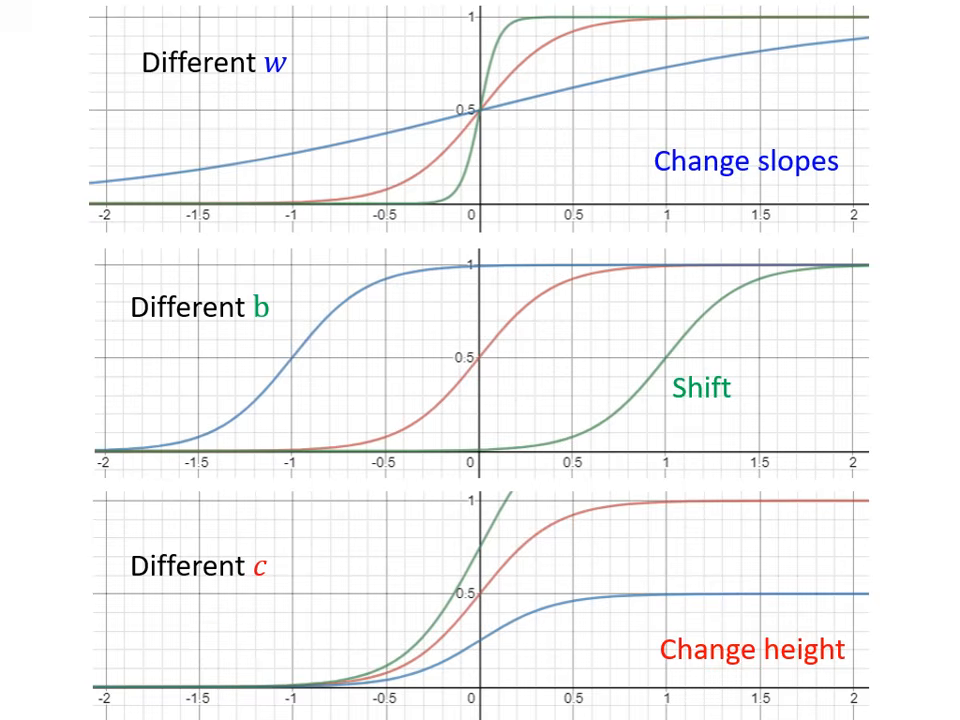
- Sigmoid 函數:
- 公式為 。
- 參數控制: 改變斜率, 改變左右位移, 改變輸出的高度。
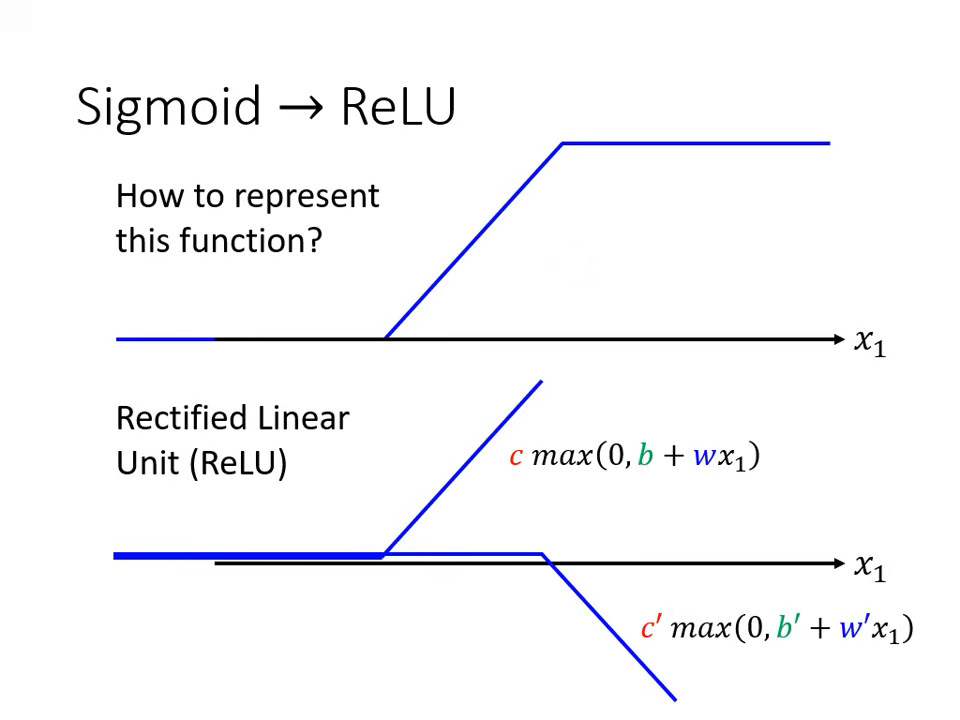
- ReLU (Rectified Linear Unit):
- 公式為 。
- 特性:一條水平線加上一個轉折斜坡,兩個 ReLU 疊加就可以組成一個 Hard Sigmoid。ReLU 是目前機器學習最常見的選擇之一。
 |  |
|---|---|
| 使用 Sigmoid 函數逼近藍色曲線 | 改變、、可以得到不同的 Sigmoid 函數 |
 |  |
|---|---|
| 兩個 ReLU 可以合成一個 hard sigmoid | Sigmoid 和 ReLU 的表示差異 |
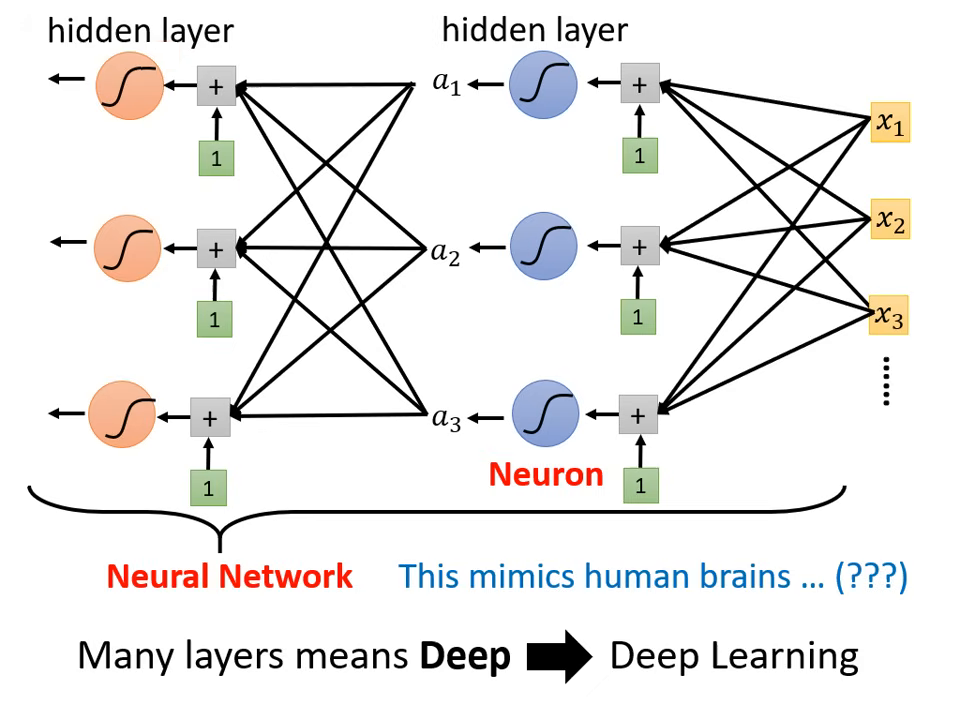
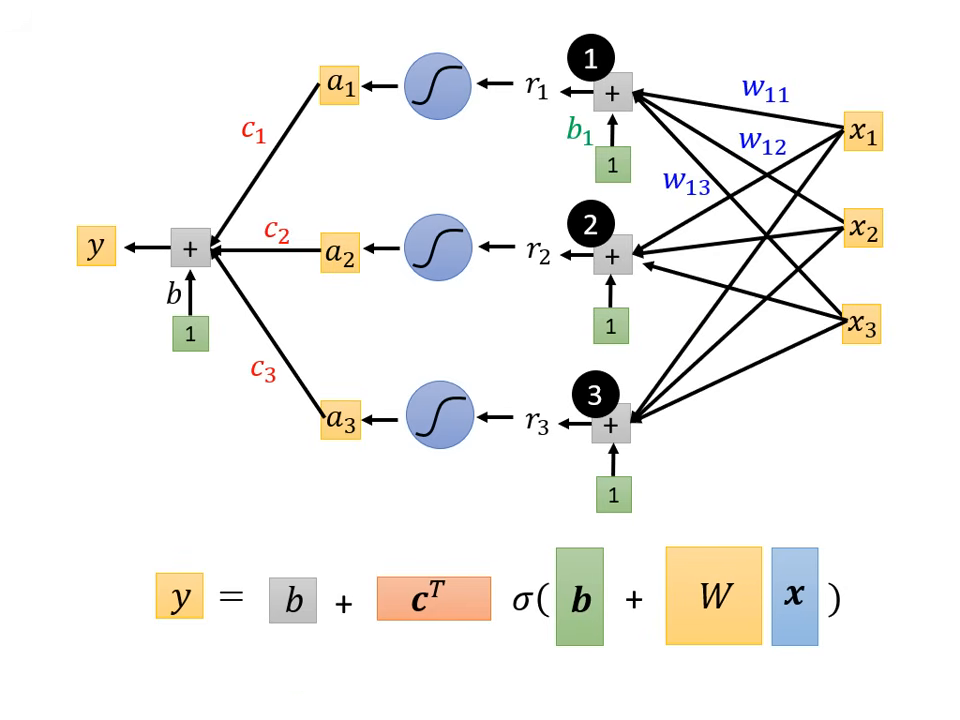
神經網路 (Neural Network)
將多個激活函數組合起來,就形成了現在的深度學習模型。
- 數學表達:將多個特徵與多組 、 進行矩陣運算,再通過 Sigmoid 或 ReLU。
- 公式簡化為:。
- 名詞定義:
- 神經元 (Neuron):一個 Sigmoid 或 ReLU 函數。
- 神經網路 (Neural Network):大量的神經元串接而成。
Loss 優化
參數的集合化:從 到
在更複雜的模型(如包含多個 Sigmoid 或 ReLU)中,未知的參數會變得非常多,包含所有的權重 、偏置 與係數 。
- (參數向量):為了方便運算,我們將模型中所有未知的參數通通拉直,拼成一個很長的向量,統稱為 。
- 第一步更新:現在的模型函式從簡單的線性變成了由 掌控的複雜函式。
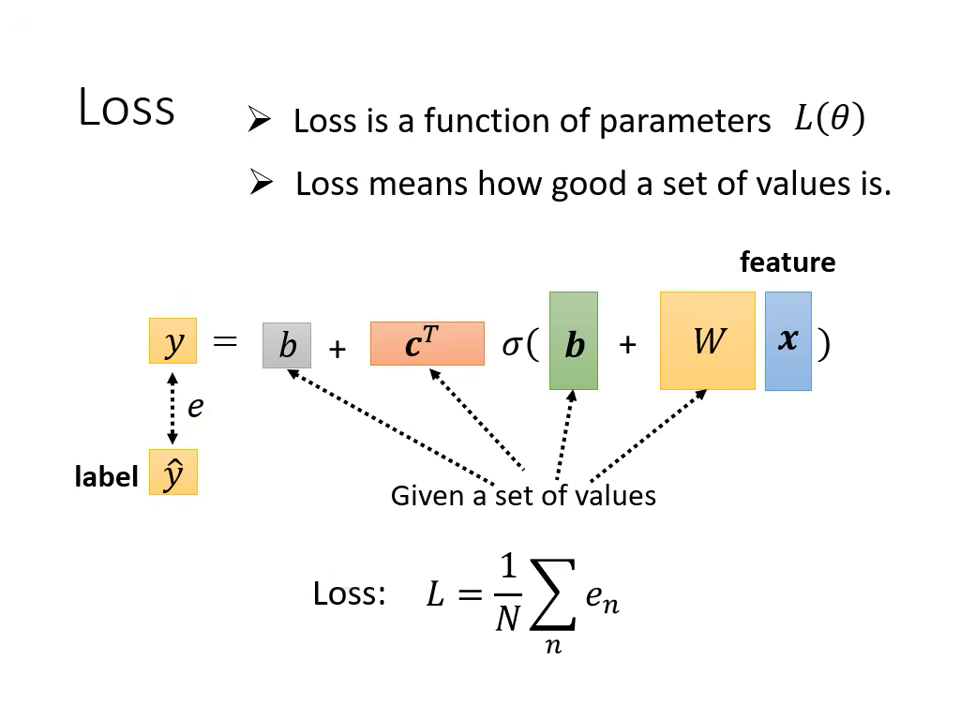
定義損失函數 (Loss Function )
定義方法與線性模型一致,但符號改為 。
- 計算流程:給定一組特定的 值,將特徵 帶入模型得到預測值 ,再計算與真實標籤(Label)之間的差距 。
- 總損失:將所有資料的誤差加總,即得到該組參數的 Loss,用以評估這組 有多不好。
梯度下降法 (Gradient Descent) 的優化流程
這是優化的核心步驟,目標是找到一組 讓 Loss 最小。
- 隨機初始化:隨機選一個初始的參數向量 。
- 計算梯度 (Gradient, ):
- 對每一個參數計算其對 的微分。
- 將這些微分值集合起來,形成一個向量,稱為 Gradient(梯度),通常標示為 或 。
- 更新參數:
- 更新公式:(其中 為學習率)。
- 這代表將 1000 個(或更多)參數同時進行更新。
- 重複迭代:不斷計算新的梯度並更新,直到不想做或梯度變為零向量為止(實務上通常是因為不想做了而停止)。
 |  |
|---|---|
| Gradient Descent 的流程 | 更新參數 |
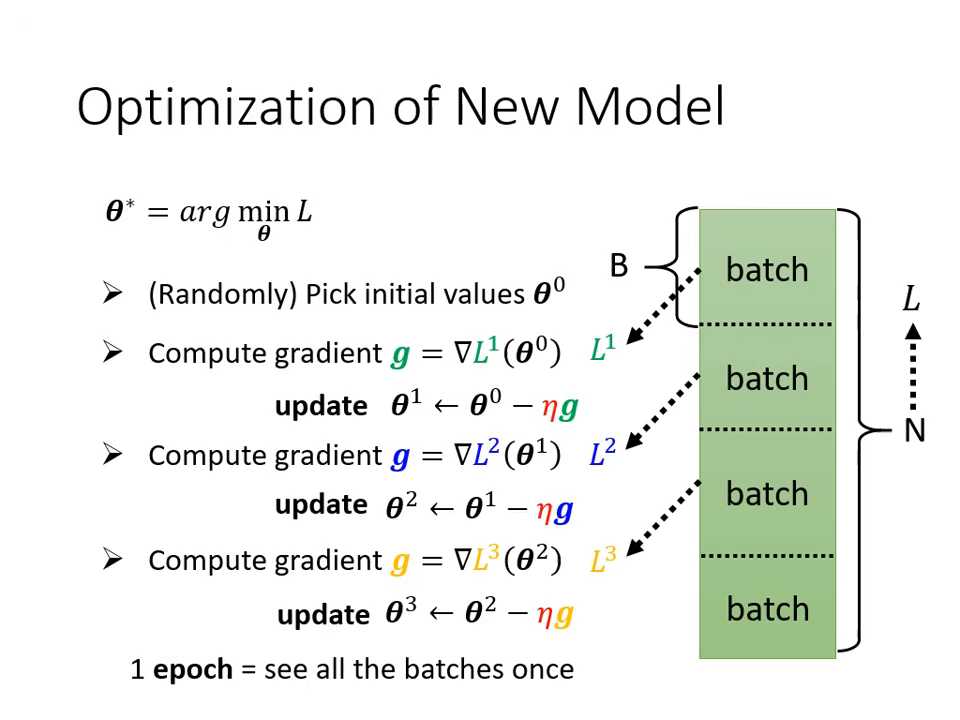
Batch 與 Epoch
在執行梯度下降找最佳參數 時,會將資料分組處理。
- Batch (批次):將總資料隨機分成多個小組。每次僅拿一個 Batch 的資料計算 Loss 並更新參數(這稱為一次 Update)。
- Epoch (回合):當所有的 Batch 都被看過一遍,就完成了一個 Epoch。
- 例:10,000 筆資料,Batch Size 設 10,則一個 Epoch 會包含 1,000 次 Update。
深度學習 (Deep Learning)
擁有許多隱藏層 (Hidden Layer) 的多層類神經網路。當神經元一層一層地堆疊起來,模型就能逐步學習由低階到高階的特徵,這種架構便稱為深度學習。