深度學習中的優化技巧 - 臨界點 (Critical Point)
在深度學習的優化(Optimization)過程中,當我們發現 Training loss 不再下降,且對結果不滿意時,往往是因為參數更新遇到了「臨界點」。
臨界點的定義與種類
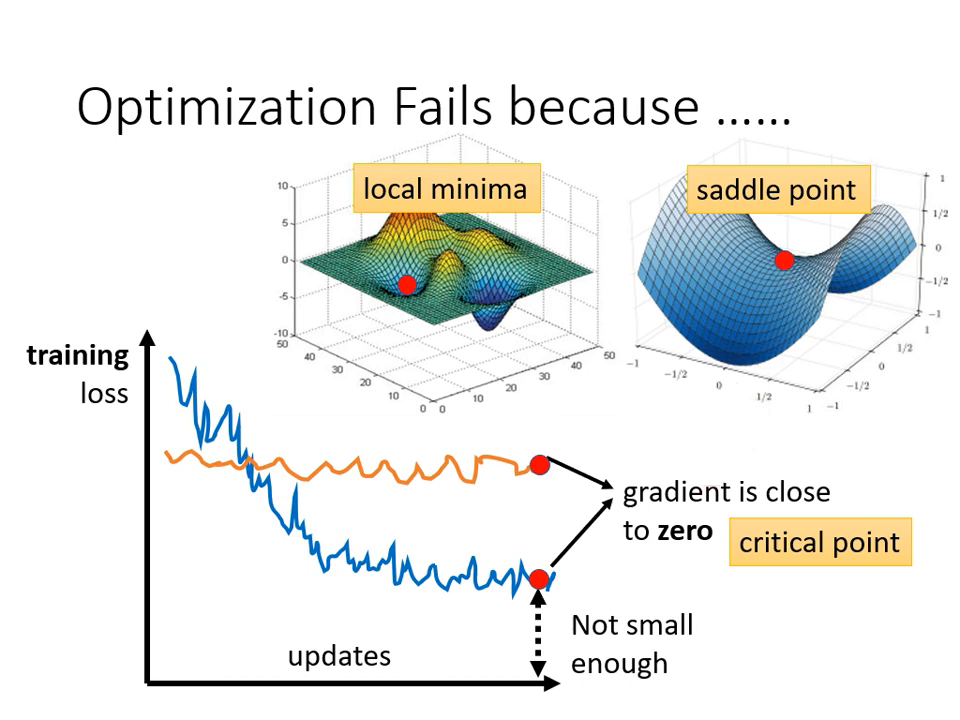
當參數對 Loss 的微分(Gradient)為零時,參數會停止更新,這些點統稱為 臨界點 (Critical Point)。臨界點主要包含以下三種:
- 局部最小值 (Local Minima):四周的 Loss 都比該點高,沒有路可以走。
- 局部最大值 (Local Maxima):四周的 Loss 都比該點低。
- 鞍點 (Saddle Point):梯度為零,但不是最高也不是最低點。其形狀像馬鞍,在某些方向 Loss 較高,但在其他方向 Loss 較低。
重要觀念: 當訓練停下來時,不要隨便說卡在 Local Minima,因為 Saddle Point 同樣會讓梯度為零,且後者仍有路可走。
數學判別法:利用 Hessian 矩陣
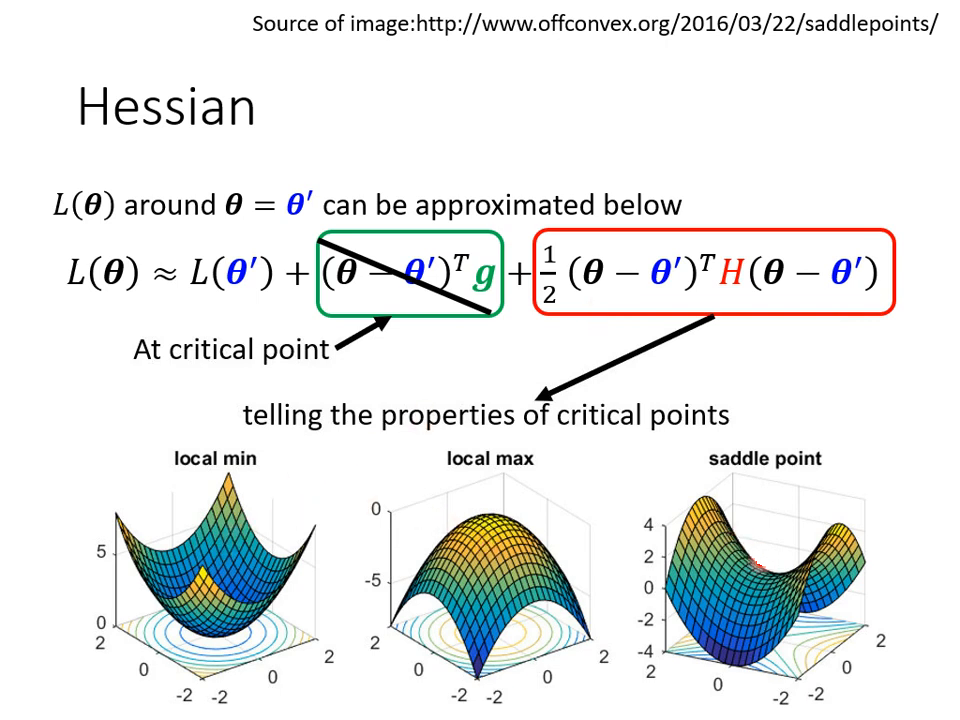
由於神經網路非常複雜,我們無法得知完整的 Error Surface 形狀,但可以用泰勒級數近似 (Taylor Series Approximation) 來得知特定參數 附近的 Loss Function 形狀。
-
泰勒級數近似公式: 。
- (Gradient): 一次微分的向量。在臨界點時 ,因此該項消失。
- (Hessian): 二次微分的矩陣,存放的是 對參數的二次偏微分。
-
根據 Hessian 的特徵值 (Eigenvalue) 判斷地貌:
- 所有特徵值皆為正 (Positive Definite): 代表該點是 Local Minima。
- 所有特徵值皆為負 (Negative Definite): 代表該點是 Local Maxima。
- 特徵值有正有負: 代表該點是 Saddle Point。
 |  |
|---|---|
| 只需考察 H 的特徵值 | 從 eigen value 判斷 |
逃離鞍點 (Escaping Saddle Point)
如果卡在鞍點,雖然梯度為零,但只要利用 Hessian 矩陣的 特徵向量 (Eigenvector) 就能找到讓 Loss 變小的路。
- 方法: 找出負的特徵值 () 及其對應的特徵向量 。
- 更新方式: 沿著 的方向更新參數 (),Loss 就會進一步下降。
- 實務限制: 雖然這是有效的方法,但在實際操作中,計算 Hessian 矩陣與特徵值的運算量極大,因此通常會採用其他運算成本較低的方法來逃離鞍點。

高維度空間下的觀點:Local Minima 真的常見嗎?
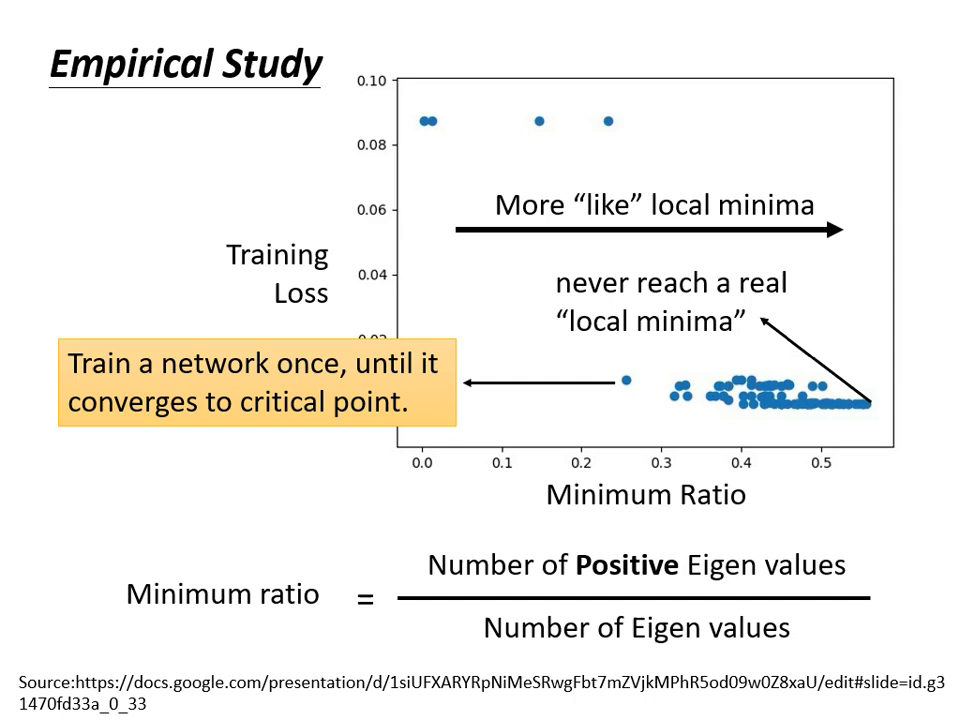
在高維度的 Error Surface 中,真正的 Local Minima 並不常見。
- 維度效應: 在低維度空間看似無路可走的 Local Minima,在數百萬參數的高維度空間中,往往只要多出一個維度,就可能變成有路可走的 Saddle Point。
- 經驗證據: 實驗顯示,多數訓練卡住的點,其 Hessian 矩陣的特徵值仍有正有負(Minimum Ratio 鮮少達到 1.0),代表我們絕大多數時候遇到的都是鞍點,而非真正的局部最小值。